[Editor’s note: this is the fifth in a series on Internet-of-Things security. You can find the introductory piece here and the prior piece here.]
There’s a good chance that every one of us knows what encryption means. Some of us probably used it as kids, if not as adults. Either for writing a note declaring that “Mrs. Chunderson is a doody-head,” to be passed to a co-conspiring classmate disguised as “Nst. Divoefstpo jt b eppez-ifbe,” or perhaps orally as, “Issuzmay Undersonchay isay uh-ay oodyday-edhay.”
The trick lies in using a code that’s hard to break – unlike those examples. History has been made more than once thanks to the art of breaking codes or the devising of codes so obscure that they were never broken (as in the case of the Navajo code-talkers).
That said, my statement confounds the similar notions of “code” and “cipher” – a distinction that’s new to me but known in the crypto-world. Codes work at the semantic level and typically require codebooks. You might replace, “The eagle has landed” with a single code “mvvpq.” By contrast, ciphers work at the character, or even bit, level. They tend to be algorithmic, making a codebook unnecessary.
So, in our discussion of encryption as it relates to computer networks and the Internet of Things (IoT), we’re dealing with ciphers, not codes.
You may also recall that the “simplistic” symmetric setup means that both sender and receiver have the same key. That’s hard in that you have to get the keys to whomever needs them, and if someone figures the key out, then you have to replace them all before things can work again.
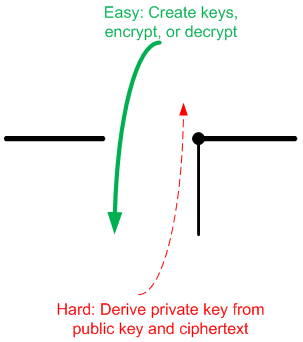
So our focus will be on asymmetric public/private key systems, and this will involve some math. In fact the math is critical in that it has to have one face that’s as easy as possible to manage and another face that’s extraordinarily hard to manage. Referred to as “trapdoor” functions, such math works well in the forward direction (dropping through the trapdoor), but trying to take an encrypted message and derive the keys and original plaintext message should be nigh unto impossible (trying to get back up through a trapdoor).
The reason you want it to work easily in the forward direction is that key generation and encryption are done as we work, and there’s only so much time that we can realistically devote to doing the calculations. If you sign into a secure website and it takes five minutes to calculate and exchange keys, followed by authentication using encrypted messages, you’re going to be unhappy.
There’s also a tradeoff between time and security. The longer the key used, the harder it will be to guess, but longer keys mean more time-consuming math. So there’s a strong desire to provide as much security as possible using the shortest keys possible.
The idea then is that a message can be converted to a number, and then some math involving the key will be performed on that number to create the encrypted “ciphertext.” Critical for making this work is the existence of an inverse function that’s hard to derive so that a ciphertext can be converted back into plaintext only by someone with the right key.
You may also recall that keys can be used two ways. Messages can be encrypted by a public key for reading after decryption with a private key, or digests can be signed with a private key for validation using a public key. Despite the use of the term “asymmetric” (which refers to the existence of two keys), the math has some symmetry built in.
There’s more than one type of math being applied to this problem, and so we will discuss three different approaches, taking them in historical order.
RSA! RSA! RSA!
The best-known and most widely used cipher is referred to as RSA (from the initials of its inventors). Of the different systems we’ll discuss today, it has the easiest math for those of us that aren’t immersed in obscure mathematical domains. Even so, it takes a bit of brain-wrapping because it’s integer math involving extremely large prime numbers and modulo division using non-trivial moduli. And there’s that bizarre totient thing. We’ll dive in more deeply on this one just to give a better idea of how it works – and because this is the most tractable of the systems.
The RSA system relies on some properties of prime and co-prime numbers (co-primes being numbers that are mutually prime, meaning that their greatest common divisor (gcd) is 1). I’ll honestly say that I’ve had to read through the details a number of times to get it to sink in. This modulo math isn’t something we do often, and, when expressed in abstract terms, you end up simply taking it on faith.
But a walk through the process illustrates the work that a system must perform when exchanging keys – as well as what the resulting encryption math will be like.
In order to create keys, you have to start by selecting two really large prime numbers – at least 512 bits, preferably 1024 bits. And as computational power evolves, the number of bits required to stay ahead keeps growing. Let’s call these two numbers p and q.
How do you come up with such large prime numbers? In theory, it’s simple: by guessing and then testing whether the guesses are prime. Turns out there is a test that works pretty quickly to determine whether a number is prime to a high degree of probability. Yeah, it’s not a straight-out true/false thing, but you can dial up the probability that you’re willing to live with, so folks operate as if it were definitive.
But in practice, it seems that some primes work better than others. So it would appear that there is a set of primes that are frequently used. This may actually be an issue, since if you can “crack” these primes, then you end up getting access to a wide variety of messages and systems. Which is a topic under current discussion in the field.
One way to address this is to use “ephemeral” keys. Instead of having a single key pair that’s frequently used, you generate new key pairs (based on a stored secret number) for different connections. This helps with the concept of “perfect forward secrecy”: if someone cracks your key today, then they can’t go back and decrypt any past messages that might have been recorded and stored.
OK, back to the basic math. These prime numbers are already large to start with. The next step is to create a modulus for all the modulo math. And it’s bad enough to have to consider modulo math with irregular moduli like 13 or 22, but here we’re going to make it even worse by creating a very large modulus as a product of p and q; we’ll call it n. So n = pq.
Next we calculate the “totient” of n. The fact that this notion exists and has a specific name boggles my mind, since, at first glance, it’s not an obvious thing of special import. Given some set of modulo integers, the totient tells you the number of numbers in that set that have a multiplicative inverse. Bet you’ve been losing sleep nights trying to find a solution to that problem.
You might think that every number has a multiplicative inverse, but we’re talking modulo math here, not real number multiplication. In fact, it turns out that a number has a multiplicative inverse with respect to a larger modulus only if the gcd between them is 1 – that is, they’re co-prime. Given a number 5 and modulus 12, 5 would have an inverse since the gcd between 5 and 12 is 1. But 4 wouldn’t have an inverse, since the gcd between 4 and 12 is 4. Obvious, no? Yeah… no.
I don’t know if there’s a general formula for the totient of any number, but for a prime number, the totient is easy: because it’s prime, by definition, there are no numbers below it that share a factor with it, so every number below it has an inverse. So for prime number p, the totient – typically referred to as ?(p) – is p-1.
Now the public key e can be selected – and, to be clear, it is in fact simply picked; it’s not calculated. It can be any prime number in the range of 3 to ?(n), where n is the modulus we calculated from p and q. Using a small number is not good for security, so, for simplicity in encrypting messages, the number 65537 is frequently used. (There’s an outside chance that number won’t work it if happens to be a factor of ?(n), but we won’t worry about that.) When you exchange keys, you send both e and the modulus n as a pair (e,n) representing the public key.
The private key is then calculated as the multiplicative inverse of the public key using a specific algorithm (the Extended Euclidean Algorithm). It’s typically referred to as d and expressed (but not exchanged) as a pair (d,n).
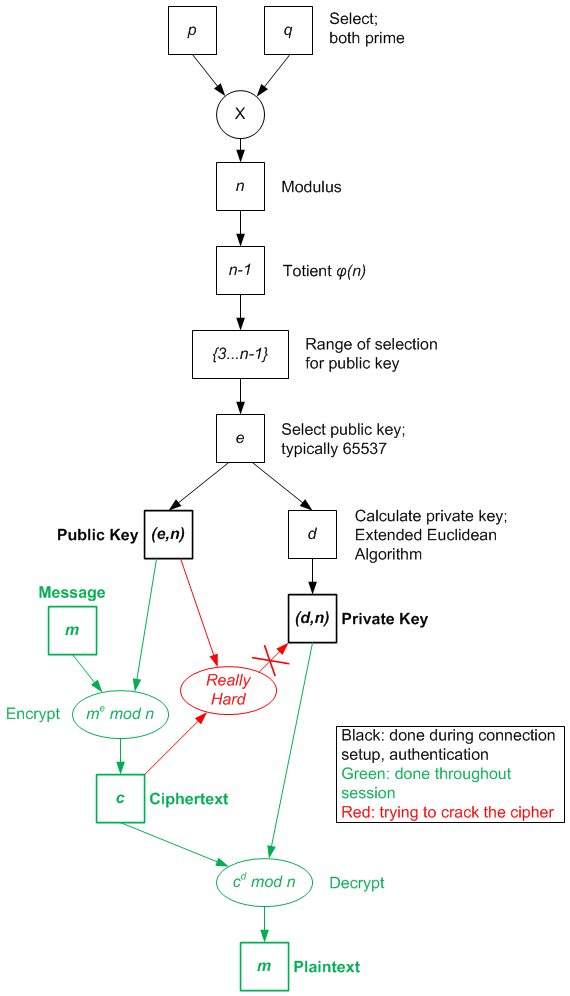
This process is sketched out in the figure to the right, where black steps indicate what happens when you start up a connection and exchange keys; green steps show the use of the keys throughout the session to encrypt and decrypt messages (could also be to sign and un-sign digests, with keys reversed). The red bits are intended to show that for an observer, who can easily obtain the public key and may be viewing an encrypted message, it’s a really hard problem to deduce the private key, which is needed to decrypt the message. That’s the nature of a trapdoor function: reasonable calculations in one direction, difficult in the other.
It also distinguishes the math needed at startup from that used during the session. For a given level of security, you’d like those calculations to be as painless as possible so that system performance doesn’t fall apart. And here’s the deal: 1024-bit keys are considered ok – for now – with RSA. But as computational power evolves, giving crackers more firepower for reversing the key, longer keys will be needed.
That same increased computational power will make it easier to work with yet longer keys than it is today, but still, if there were a way to reduce key size without compromising security, that would help to reduce power, if nothing else. And if we’re talking IoT edge nodes with constrained resources, then we have every incentive to keep the math as easy as possible (in the forward direction).
Avast, ye curvy knave!
More recently, elliptic-curve cryptography (ECC) has come onto the scene as an alternative to RSA. And the first thing that needs to be said about this is that it has nothing to do with ellipses of the Kepler variety. There’s a historical link to ellipses (something about calculating an ellipse’s arc length), but you need to banish those little ovoids from your head.
In fact, non-obviously, an elliptic curve is defined by the function, y2 = x3 + ax + b. It’s defined on a “finite field” (or a Galois field) – in other words, this isn’t a normal real-number concept. And if we really want to understand this, we need to descend into the depths of obscure mathematics. Just to give a flavor, for a more precise sense of finite fields, here’s its “is a subset of” hierarchy according to Wikipedia: “Commutative rings ? integral domains ? integrally closed domains ? unique factorization domains ? principal ideal domains ? Euclidean domains ? fields ? finite fields.”
Yeah, I’m not even going to try to dissect this one. But here’s the deal: there’s a concept of “point multiplication,” and reversing it is a very hard problem, as yet unsolved. Point multiplication refers to taking some point P along the curve and adding that point to itself some number of times n to get a result Q. The success of ECC relies on the fact that, given Q and P, it’s really hard to figure out n.
And the benefit of all this is that, for a given level of security, you can use a shorter key with ECC than with RSA (like 256 bits instead of 1024). (Or, if you went with 1024 bits, you’d have more security.) So ECC is working its way into our systems as it is accepted as a successor to RSA.
Note that the equation defining an elliptic curve represents a family of curves, depending on a and b. And, apparently, not just any curves will do, and some yield to easier forward calculations that don’t violate patents. So part of the vetting process for this system has involved finding curves that work well and then standardizing them. So, in the fine print on your encryption engine, you may find comments regarding specifically which curves are supported.
The more you try to erase me
But ECC may not be the end game. There’s a newer concept making the rounds, offered up by a company named SecureRF. They call their approach the Algebraic Eraser. (And yes, they have patents.) The math here starts to feel even more obscure than ECC: it exploits the concept of braid theory.
Braid theory has to do with operations performed on braids, where manipulations are performed on strings that are fixed at the end but movable in the middle. Of course, it’s rather abstracted and turns into a matrix math problem in the end. Secure RF has some whitepapers in place that describe much (although not all) of what’s going on. They appear to have added some more papers since I first looked, so that makes understanding a bit easier. (In a relative sense.)
The point of this approach has to do with the resources needed to do the necessary calculations. In particular, if you’re doing this stuff in software, your basic temperature sensor with wireless probably isn’t going to be outfitted with a huge processor, and SecureRF suggests that the math required both for RSA and for ECC are beyond what tiny edge nodes should be expected to do. In particular, they say that 8- and 16-bit processors cannot handle ECC math, but can handle Algebraic Eraser math.
They’ve implemented the algorithm as FPGA IP for inclusion in prototypes and evaluation. They also have software implementations ready and a silicon implementation in development.
This brings up a couple of points. The first has to do with how security is implemented, and it’s generally said that hardware is far more secure than software. Why? Because software can be monkeyed with, and data in use in main memory can be snooped. Hardware, by contrast, does what it does far from the prying eyes of bus sniffers and such.
There are chips that implement encryption algorithms in hardware. So it’s not a given that a microcontroller would have to have enough computing resource for encryption: all of the calculations could be offloaded to a crypto-engine. But storage is also an issue: longer keys result in longer ciphertexts, so an ECC system, for example, could be equipped with less memory than would be required for RSA.
So part of the process of adoption (if it happens) of Algebraic Eraser involves understanding not only how well it secures a system, but how it competes on cost and power.
Which leads us to the other consideration: how does the industry decide to use a new encryption approach? I talked to SecureRF, and it turns out that they’ve been working on this for ten years, and the “approval” process is slowly grinding along.
The thing is, though, there’s no “formal” or “official” approval. You present your ideas at conferences attended by important crypto-folks, and they start to stroke their beards and ruminate on what they’re hearing, and they go away and start pushing on the math and pulling on the implementations and publishing their results. Over time, if all goes well, a body of work emerges that gives everyone confidence that yes, this does work.
Apparently, there are folks who don’t want to wait that long: SecureRF says that they have customers who want Algebraic Eraser now. But others are going to wait for a few more votes of confidence before jumping in; the most conservative will wait until full-blown endorsement by the highest authorities – groups like NIST.
So this is a flavor of how keys are derived and used in any system that requires secrecy. And that would include every node on a huge IoT network where access through a minor innocuous port can lead to a rich trove of information for someone who knows how to burgle such a network. And it affects how architects and designers will implement that security to both protect the goods and keep network nodes cheap and power-stingy.
But these keys work only because the private keys are secret. And secrets are useful only if they remain secret, and you know that there are people for whom secrets are the ultimate temptation. As long as the secret remains secret, they have failed, and they hate failing. So keeping the keys secret is important – and yet you’d be amazed at the lengths crackers will go to ferret them (and any other secrets) out. So next time we’ll look at some of the considerations for protecting those secrets from unauthorized eyes.
[Editor’s note: the next article in the series, on key protection, can be found here.]
More info:







Do you know of other approaches to encryption that can be of benefit to systems with few resources?
Some interesting facts and puzzles about Prime Numbers and Magic Squares, Smith Numbers, and Arithmetic and Palindromic Primes on this blog: http://www.glennwestmore.com.au.