“I need a brush.”
What would you do given such instruction by someone to whom the response, “Can you be more specific, please?” would be considered inappropriate? It’s a hard request (or demand) to satisfy if you know absolutely nothing about his or her intent. It’s almost as bad as the “Bring me a rock” theory of management, except that that’s simply a way of ensuring that your employees are never quite sure if they’re doing the right thing, and so they remain nervous and stressed; putty in your hands. No, in this case, we’re just assuming poor communication skills, nothing Machiavellian.
So you would have to do a lot of work to cover all possible bases. Is he or she looking for a toothbrush? A paint brush? A hairbrush? A brush on a non-brushless motor? Probably not looking for a shrub (that would be “Bring me some brush,” unless not proficient in English – then this might also be a possibility).
The point is that when you know the intent, you can be much more efficient about satisfying the request. It’s a particularly useful tool for customer support: “Can you do xyz?” “Well, what are you trying to accomplish?”
But even if you knew that a toothbrush was intended, that still doesn’t give you enough information to guarantee success. Hard bristle? Soft? Those goofy fatty bristles that make the thing look all tech and add $3 to the price? Knowing that it’s a toothbrush at least gets you to the right place to purchase one, but you still have several parameters that must be filled in to guarantee that you get the right toothbrush.
This concept has been used extensively in EDA for circuits; it’s what abstraction is all about, especially for digital blocks. Given intent, you know how a particular transistor is going to be used, and you no longer need to model all of the details of the transistor; only the ones that matter, and those are pushed up to the block interface as higher-level values and parameters. This allows you to make simplifying assumptions, and the math “degenerates” as components drop out of equations.
While this may be commonplace for electronics, it’s less so for mechanical design. After all, if you’re going to create a new custom shape, you pretty much have to model it at the lowest level, going to first (or close) principles to get all of the stresses and fields and temperature fluxes right. So, at their most basic, mechanical CAD tools allow you to specify a 3D object either in all three dimensions or by defining a 2D object and then extruding it into a third dimension. Simulation then takes place using finite element analysis, and, for best accuracy, the number of points to be modeled can be very large.
But MEMS is a very specific type of mechanical design, and the number of possible ways a given structure might be used drops dramatically. This opens up the possibility of letting the user express intent by selecting specific elements and then supplying a few remaining parameters.
When I sat down with Coventor at the MEMS Executive Congress and discussed their latest 3.0 MEMS+ tool release, there were a number of fundamental things that seemed worth digging into. Most elementary was their library of elements: what do they consider to be the base set of structures for MEMS? There were also some new modeling concepts that felt useful to explore.
From a high level, having a library might simply be seen as a timesaver: you don’t have to draw this element; just pick it from a list and then carry on as if you had drawn it from scratch. But, in fact, it’s more than that. Picking a library element now specifies intent: it’s not a random shape, but one with known properties when used in a typical fashion. This allows both simplification as coefficients zero out and greater accuracy of the calculations that matter.
Simply put, the items you pull from a library degenerate from more general models. And in most of what we’re going to discuss – with one specific exception – that becomes the benefit. It’s good to be a degenerate (no matter what your mother said) because it makes life much simpler. The underlying analysis still uses finite elements, but calculations can be reduced by orders of magnitude.
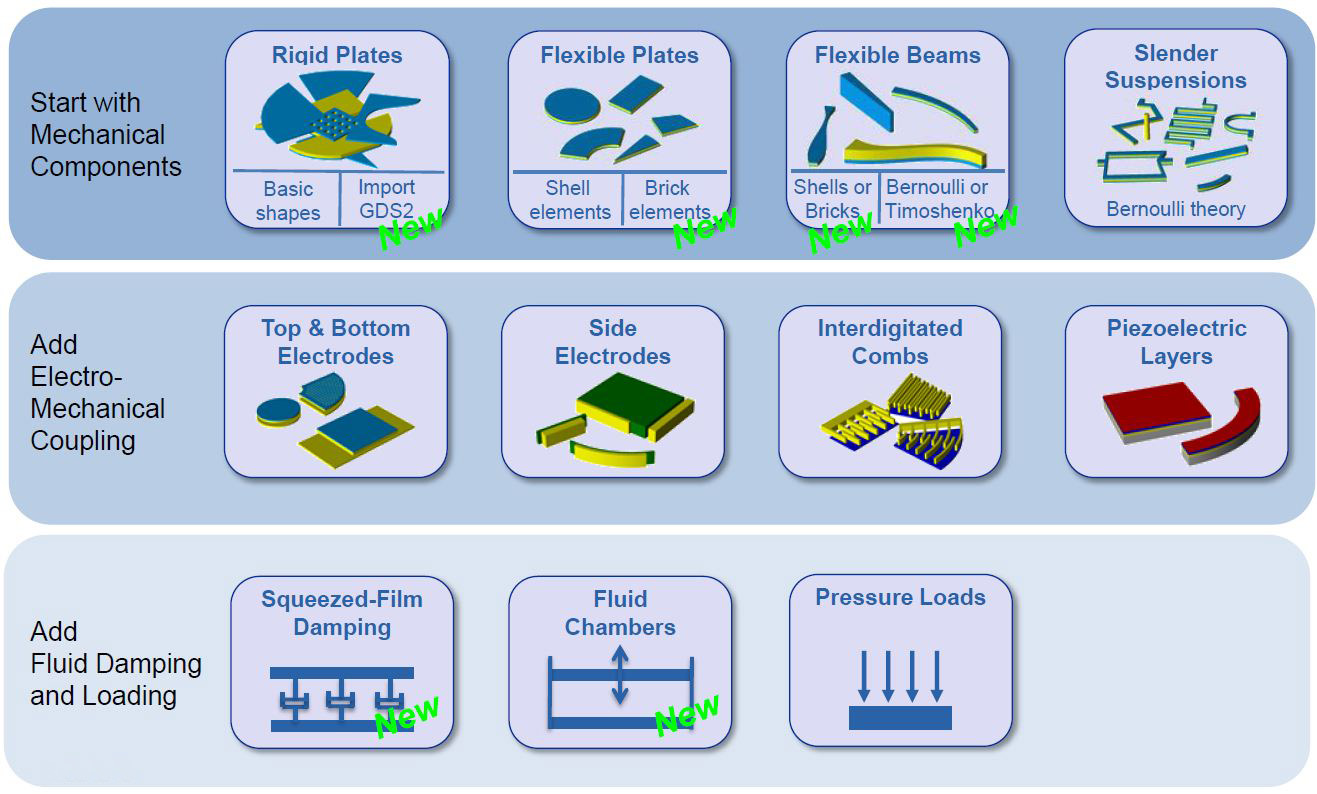
Coventor’s library itself is divided into three groups: mechanical elements, electro-mechanical elements, and fluid elements. Each of these has sub-categories.
(Courtesy Coventor)
The simplest of mechanical elements are the plates. That is, something that can be drawn in two dimensions, with the third dimension being the thickness of the film or material from which the plate is formed. But even here, there are two groups: rigid and flexible plates. Rigid plates are degenerate flexible plates; plate deformation doesn’t have to be considered. To give an idea of the savings that this produces, a rigid plate can be modeled with six unknowns. In the absence of this expression of intent, there could be tens or hundreds of thousands of unknowns to solve for.
If you need to consider non-rigidity, there are two types of model that MEMS+ now supports: so-called “shell” and “brick” models. Shell models look at first glance like degenerate brick models: they don’t use nodes on the top and bottom; just along the center. They’re therefore more appropriate for elements having large x/y extent, with z playing less of a role.
Brick models, by contrast, model the third dimension more explicitly. This trades increased accuracy and modeling flexibility for longer analysis time. Brick modeling is new in the latest MEMS+ version.
It may look like a shell is a degenerate brick, but that’s not strictly true from a mathematical standpoint. The savings in the shell model are not due to the collapsing of big equations into smaller ones: according to Stephen Breit, shell mathematics are actually quite different, with their own complexity and sophistication. So shell modeling approaches are not obvious from brick modeling.
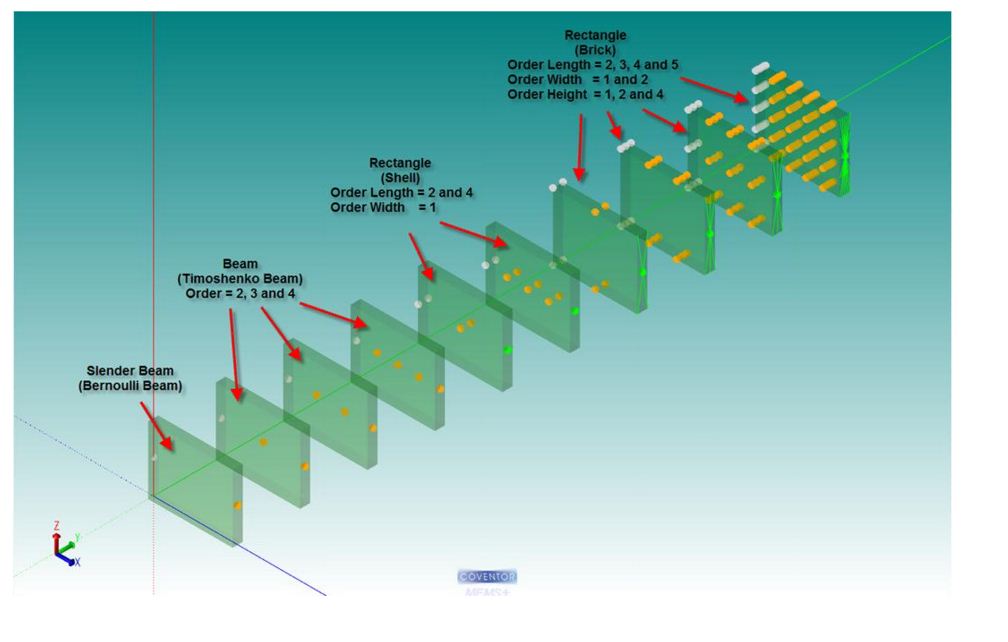
Beyond plates, we move to beams, which are long slender elements that may be supported on one or two ends. These also have two different modeling approaches. The simplest is Bernoulli modeling, which assigns a node to each end of the beam; each node has three degrees of freedom (DOF). This breaks down for shorter beams or where more sophisticated “behaviors” like torsion are to be considered. Then Timoshenko modeling is used, again trading analysis speed for accuracy. Timoshenko modeling is new in MEMS+ 3.0.
The increase in complexity is illustrated in the following figure from Coventor. The simplest model is a Bernoulli beam model; Timoshenko modeling with order 2, 3, or 4 follow. Beyond that, the beam is shown modeled more generally as a rectangle using a shell model with the width of order 1 and the length of order 2 and 4. For greater accuracy yet, a brick model of the beam can be specified, now working on all three dimensions up to fifth order.
(Courtesy Coventor)
The last category of mechanical structure is called “slender suspensions.” These are really assemblages of beams. In theory, you could build them yourself by affixing beams to each other, but by selecting them from a library, you don’t have to take the time to build them, and the number of nodes to calculate is reduced, since the interfaces between the elements can be “smoothed” or simplified. For the time being, these devices are simulated using Bernoulli beam models.
Next we move into the electromechanical realm (which is, of course, the EM in MEMS). The simplest elements here are electrodes, but they distinguish top/bottom electrodes from side electrodes. This is because of the way MEMS devices are built: layer by layer. With top/bottom electrodes, you’re drawing the shape on a layer; this can be bigger or smaller than the MEMS element to which it’s providing contact. The only other main parameter needed is the layer on which it will be drawn.
Side electrodes, by contrast, have a fixed height determined by the thickness of the layer from which they’re formed; this makes them easier to create. It also says that that the electrode height cannot be different from the height of other elements made from that layer; unlike top/bottom electrodes, there’s no over- or underlap possible in one of the two electrode dimensions.
Combs are extremely common structures since they are used for capacitive sensing and actuation. It’s simply natural that such a pain-to-draw element be available from a library. Piezoelectric layers are the last category, also common for both electromechanical actuation and sensing.
Finally, fluid analysis is increasingly required in order to fully understand how a MEMS element will behave. Coventor has modeled pressure before but has now added two more sophisticated types of fluid behavior in order to capture the effect that gasses – or their absence – have on moving structures.
The simpler of the two is the fluid chamber, used primarily for modeling microphones. It assumes that the pressure is the same everywhere. By contrast, the squeezed-film element captures both spring-like (lossless) and damping (lossy) behaviors, and it allows for the pressure to be different at different points in the chamber and for the dynamics of propagating pressure to be analyzed.
All of these elements have context-appropriate parameters that generalize the shape of the element – while fixing everything else. You can specify the shape of a rigid plate, but you can’t specify a stress/strain parameter for bending because then it would no longer be rigid. But, in a nod to MEMS manufacturing, all shapes have one parameter that would otherwise look odd: perforation. This accommodates element release when needed.
As mentioned, even though expressing intent through library element selection simplifies a lot of math, it also has provided Coventor with the opportunity to drill in hard so that the math that remains is accurate. In fact, it’s probably more accurate than what you’d get if you tried to build the element by hand. And, in some cases, it may be more accurate than needed. So they allow degrees of simplification, much as you might find in the circuit world. You can use high accuracy for small elements – like using SPICE for individual transistors – but then go with a simpler model for full-system analysis – like digital simulation.
In many cases, a simpler model will do – but well-schooled mechanical designers may be skeptical as to whether the accuracy is good enough. The availability of the more complex models can often help to convince such designers that, in fact, the simpler model is adequate and can save significant computation time.
The other reality is that these mechanical elements are going into electronic systems. Localized mechanical models will eventually be imported into EDA tools from companies like Cadence, and the users of such tools typically have no patience for long, drawn-out simulations. The simpler models help to make these guys happy as well.
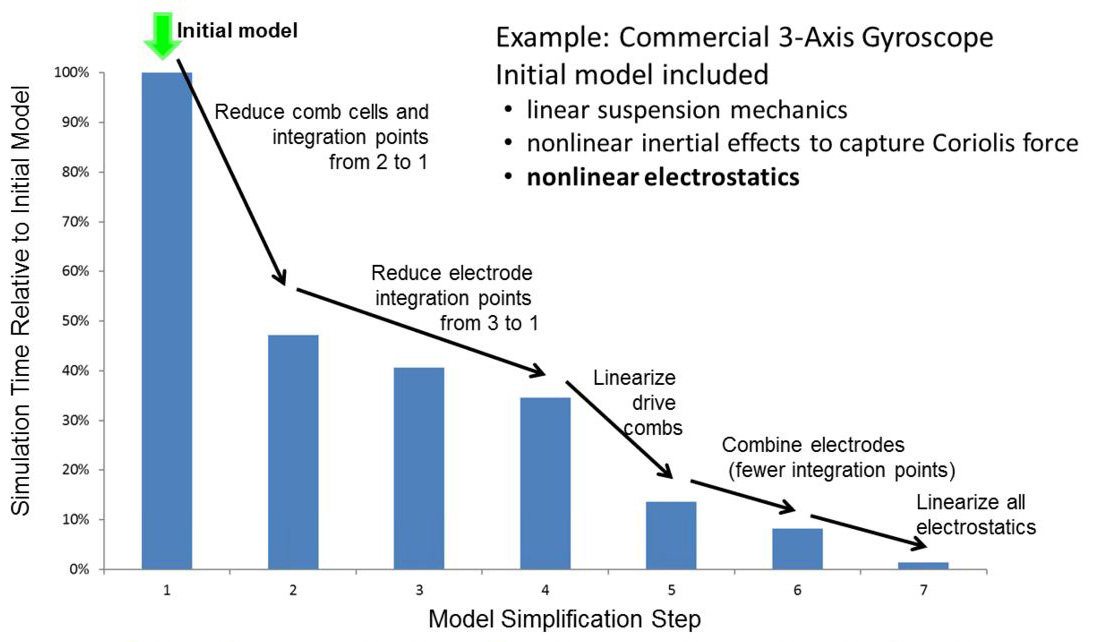
Coventor shows one example of a gyroscope model that started as very complete and complex and was gradually simplified, yielding an almost 50X improvement in simulation time.
(Courtesy Coventor)
This flexibility to work with complex or simplified models is ultimately brought to you by one simple concept: intent. Because these elements are intended to be used in very specific ways, both drawing and analysis time can be shortened dramatically. It brings mechanical – and electromechanical – design much closer to what we’ve been used to for years in electronic design.
Now: go get that brush, you degenerate.
More info:






Here we looked at how Coventor’s element ontology. How does that square with how you see the world? Do you organize things the same way or differently?