Perhaps you’re new to the US and you’re investigating some recipes to make. You’ve resigned yourself to the fact that, here, things are measured more by volume than by weight, and the measurement units have that peculiar non-metric feel about them that forces you to prove you can still do mental arithmetic. But the terms for things are sometimes different too, even if you come from another purported English-speaking country. We don’t do aubergines and courgettes; we do eggplants and zucchini.

But terms can vary even within the country. Perhaps there’s this one dish you’re researching online, and one version will call for green onions and another will call for scallions. Without too much work, you could sleuth around to find that they are one and the same. But neither recipe, on its own, is willing to make that clear for you. If you don’t chase it for yourself, you’ll end up confused.

Today’s tech story has a bit of a similar feel, except that the ending is a tad more tentative. We’ll start where I started, by noting that an increasing number of conference presentations have been making reference to memristors. Time to get a better sense of what they are.

Back in 1971, Prof. Leon Chua of UC Berkeley, a (some would say “the”) recognized authority on non-linear circuit theory, noticed an absence of symmetry in the panoply of fundamental two-terminal circuit elements. Resistors relate current and voltage; capacitors relate voltage and charge – which is the time integral of current; and inductors relate current and magnetic flux. The missing piece was something relating charge and flux.

And so he made a theoretical, mathematical observation that there could be a fourth element that related charge and flux; it would have an I-V curve that had a characteristic butterfly shape. Critically, the device exhibits hysteresis, and, depending on its history, it might behave as if it had one resistance or another. From this behavior, where resistance depends on remembering its history, he whimsically dubbed it a “memristor.” The shape of the I-V curve has been dubbed a “pinched hysteresis loop.” The differential form of the equation is

dφ = Mdq

where M is the memristance. Here, flux doesn’t necessarily refer to the physical mechanism of magnetism, but rather a more generalized time-integral of voltage.

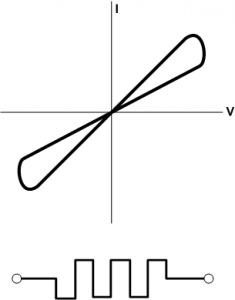
Memristor I/V curve – the pinched hysteresis loop – and circuit symbol

It was a mathematical novelty, not really anything anyone wanted to jump on and do anything with. It wasn’t trumpeted as a brash new discovery; just a side note of nominal interest and perhaps no practical value.

That all changed in 2008 when a team at HP ran across that equation and realized that it described some behavior they had been seeing in titanium oxide, TiO₂. And they announced, to great fanfare, that they had found a real-life memristor.

The way they made their memristor was to layer two thin films of TiO₂ between two platinum electrodes. One of the films was doped with extra holes and had lower resistance. As a voltage was applied across it, oxygen vacancies drifted, moving the boundary between what appeared doped and undoped to the left or right, depending on the voltage direction. That changed the thickness of the relatively less-resistive portion of the film, changing the overall resistance. The longer it went – in other words, the more current flowed over time, aka the more charge went through it, the more the vacancies drifted (to a point), and the more the resistance changed – that is, the resistance depended on the current history.

Importantly, this is a non-volatile effect: once the voltage is removed, everything stops, and the device “remembers” where it is because the oxygen vacancies stay put. Note that this “state” is very hard to perturb accidentally: it’s unaffected by things like radiation and therefore has the potential to be stable over long periods of time.

They determined the memristance M to be as follows:

where µ_V is the dopant mobility and – critically –D refers to the TiO₂ film thickness. And this explains why this effect hasn’t been seen before except as a 2^nd-order (or smaller) anomaly that has been hard to explain: it defaults to resistance as thickness increases. Much as relativistic and quantum effects degenerate to Newtonian laws at everyday dimensions, so does this.

One other nice thing about this device is that, theoretically, you could create an array of these with rows connecting one side and columns connecting the others and address any of them without using a select transistor. Sounds like a nice way to make a very area-efficient memory. But… that’s getting slightly ahead of things here. Before we pursue that angle, we need to step back a bit.

I started by noting the increasing appearance of “memristor” in conference presentations. Subsequent to looking into them, I also noticed many references – in particular at IEDM – to resistive memory, or RRAM (or ReRAM). The obvious question then becomes, how does such resistive memory relate to a memristor, which also relates concepts of resistance and memory?

I mentioned that HP’s “discovery” of the memristor came when they related Prof. Chua’s equations to effects they had been seeing. In fact, there has been work on resistive elements for memory, often referred to as “resistive switching,” dating back to the ‘60s, long before the concept of a “memristor” had even been dreamed up.

A variety of materials have been studied, notably a class of materials called perovskites (particularly SrTiO₃ – or STO – and SrZrO₃ – or SZO), various transition metal oxides, and other so-called “molecular materials” exploiting conductive filaments, interfacial effects, and trapped charges. In fact, the list of materials I saw that had been investigated included AlOx, HfOx, TiON, Te₂O₅, TiOx, NiO, CoO, and WOx.

Some of these materials form filaments that move up and down inside the material; others become more generally conductive. Some of them have the same polarity voltage that sets and resets their resistance – so-called “unipolar” cells, typically involving inert materials like platinum and gold – and some require voltages of opposite polarity to set and reset the cell – so-called “bipolar” cells, typically involving reactive materials like Ti, Ta, and TiN.

Each material may contribute some different property to the structure. With some you can reverse the electrode contact between ohmic and Schottky as the dopant drifts. TaOx with platinum electrodes has exceeded 10¹² cycles of endurance. Hafnium holds the potential for multi-level cells – and is also very CMOS-friendly.

Of note, however, is that in many of these, the drifting of oxygen vacancies plays an important role. Sound familiar? It did to me, but, maddeningly, in almost none of the RRAM papers was there any mention of the word “memristor.” Was TiO² the only “true” (a loaded word, as we’ll see) memristor? Was there some detail that made the other materials not memristive? Or were they also memristive but for some reason no one was mentioning that?

So I looked around for expert opinion to try to referee the situation – which proved harder than I thought (since much of industry focuses on technologies that are manufacturable today – or at least soon, which this is not). I had one conversation with Cadence’s Steve Leibson, who’s been watching the technology.

His view is somewhat practical, by his own admission: he doesn’t really care what you call anything; the question is, is it manufacturable, cost- and power-effective, etc.? If you take RRAM to mean anything that uses a shift in resistance to determine state, then even things like MRAM and phase-change memory (PCRAM) are included.

More interestingly, he alluded to some controversy as to whether what HP found was even a memristor at all – making sure to clarify that this wasn’t his position, just that he was aware that there was some debate; we left it there.

Following that thread uncovered more than one disagreement regarding these topics. Some of it pretty hot – one ex-USPTO person with a background in the space charged that what HP had found was decidedly not a memristor, but more of a publicity stunt – and that Prof. Chua had been drawn in to save face for HP.

Much of the discussion focused on “memristive systems” vs. “memristors,” and I’ll admit that the distinction gets pretty opaque at times. Meanwhile, Prof. Chua wrote a new paper last year that generalized the definition of a memristor to be pretty much anything that showed the characteristic pinched hysteresis loop, regardless of the underlying mechanism. Spin-related mechanisms such as are exploited in MRAMs can count as memristive.

Further conversation with Kilopass’s CTO Harry Luan helped to clarify some of this. One of the complaints you’ll find is that no one has found an “ideal” memristor. And my response to that has been, well duh, we don’t have any ideal resistors either: they all have capacitance and inductance and other non-ideal behaviors. For instance, an ideal resistor would relate only I and V, and yet, in a real-world resistor, temperature also matters.

So here’s where we refine our definition of “ideal.” Yes, parasitics and environmental variables affect resistors and memristors. But even discounting that, there’s still an issue with real-world memristors, and it gets to the concept of “state” – as does anything involving history or memory. Ideally, as originally defined, the state of the memristor refers to the amount of charge that has passed through. But the overall state of real-world memristors seems to involve more than just charge. This is where “memristive system” was distinguished from “memristor.”

However, by generalizing the definition of a memristor, the exact nature of the state is no longer of primary concern, and so the distinction between “memristive system” and “memristor” has pretty much gone away. Not that everyone is happy about that.

At the same time, mathematical discussions have proposed other components like memcapacitors and meminductors – and there is debate as to whether those are primary or secondary or whatever. More to churn on.

So how does this all wrap up? Well, RRAMs exploit resistance-switching phenomena, some of which may be memristors – as originally defined. The new definition is general enough to where it’s likely that most RRAM cells will qualify as a memristor (with some folks still objecting). The promise of having no select transistor is still unmet at high densities.

As to the two technology threads that didn’t seem to acknowledge each other, RRAM folks have been concerned with making practical memories for decades; memristors started as a mathematical curiosity that stayed under the radar until recently. There’s only recently been something of a forced rationalization of the definitions as the debate has raged.

So hopefully it’s now a green onion/scallion thing. I’m not sure I’m willing to place money on that, however…

More info:

An interesting discussion of the recent debate